My Favorite No
One of my go-to and favorite activities is the error analysis task of My Favorite No. Originally created by Leah Alcala from Berkeley, California, this is a task that I use often with my students. I have often looked through my Activity Builder (AB) answers and have seen some creative, but incorrect answers from my students. In looking through the answers, I find one that I can tell what the student was thinking and what misconception they have regarding the topic. I take a screenshot of the solution and the question that it answers and use it as a question for the class to discuss.
In the Point Collector AB, one of my students gave this graph as a possibility in scoring the highest amount of points. Just a reminder that this activity explores linear inequalities and red points score -1 while blue points score +1. This student’s answer was thoughtful but could they have scored more points? How might we change their equations to maximize their total score?
I pose this question to the class and give them time on their own and then time in small groups to discuss and, possibly, create a new solution. This method gives all students an opportunity to make errors, analyze those errors, and then discuss may change.
Warm-Ups
Another option of using student responses is creating a warm-up question for the class following the Point Collector: Lines AB. I create a Google Slide of the question and have it posted when my students enter class.
The question from the AB:

A student answered:
Do you agree with this student? Why or why not?
This question was from an AB that I created to introduce using square roots to solve quadratics. I found that, during the activity, many students appeared to understand the concept but were not being precise in their answers. I took this opportunity to create a warm-up for the following class to help my students understand that precision in solutions in important in math, especially when they are trying to support more basic solutions. The previous question asked students to graph the equation y=x2-5. Its purpose was to have students discover that not all intercepts are integral. I also wanted students to see that there is a relationship between the number of x-intercepts of the graph of the equation and the number of solutions. The question I posed to the class was, “ Explain this student’s explanation. Do you agree/ disagree? Would you change it?”
Stretch Thinking
I often have students who finish assessments and activities early and I like to have something to give them to stretch their thinking. The screenshot below is from the Point Collector: Lines activity. I could offer the question, “What may be the inequalities that this student used to solve this problem?” There are multiple solutions to this which all are advanced thinking for my students.
Snapshots
While I was writing these posts, Desmos revealed a new feature: Snapshots. While I have not yet used this feature with students, I see a world of opportunities by using student solutions to create further discussions in class. Snapshots can be reached on the Dashboard in the Teacher view.
In clicking the camera icons next to student solutions, a notification appears at the top of the screen.

A teacher can drag and drop the Snapshots onto the right side of the screen to create a collection. You are given an option to write a question that will appear with the Snapshots when they are presented.
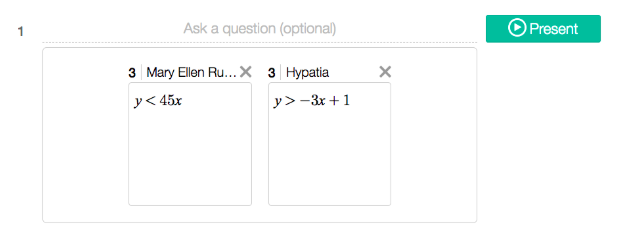
When present is selected, you see your Snapshot collection along with your question (if entered.)
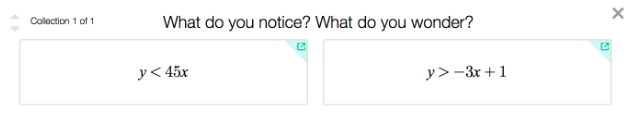
I feel that opportunities are endless with this new feature: you could pause an AB and ask questions of the class, you could ask questions at the end of class without needing much prep to create the presentations, or you could create a collection with questions to use the next class as a warm up or check-in. I would love to hear how you all may use this new feature!
Up Next: Game Playing to Create a Need for Vocabulary and Discussion
#Desmos
#MTBoS